51-附录六：轻松搞定位运算

一 前言

位运算，一个极容易被低端码农忽视的地带，因为它略微需要用一丢丢智商，真的只有那么一丢丢，但高手与low手的差距往往就是长这么一丢丢，能达到的深度就截然不同了，今天egon就来给大家聊一聊位运算那些风骚且高级的操作，但要理解位运算，得从机器数与真值说起，请看大屏幕

二 真值、机器数(原码、反码、补码)

“真值”指的就是数本身，例如-10，真值就是-10

一个数在计算机中的二进制表示形式，叫做这个数的机器数

在计算机中，用来表示有符号数的机器数有三种，即原码、反码、补码

三种表示方法均有“符号位”和“数值位”两部分

1、符号位都是占据最高位，用0表示“正数”，用1表示“负数”
2、数值位，三种表示方法各不相同

整型数字有8位、16位、32位、64位几种，篇幅问题，我们先单以8位整型为例来介绍

在介绍之前，egon先来先扫一下盲，估计会扫死99%的人

问：8位二进制数可以表示的数值范围是多少，99%的人张口就来：-128~127

ok，8位二进制数，最高位需要用来表示符号，那么剩下的7位用来表示数值

于是，最大数为1111 1111=>+127，最小0111 1111=>-127，卧槽，得出的结论是8位二进制数可以表示的数值范围是-127到+127，傻逼了吧你，哈哈哈

灵魂拷问：-128到底怎么来的？？？

 真相是这样的：
  8位二进制数用7位表示数值，那么7位2进制数000 0000的值为0
  那么,它前面加上符号位0,还表示0吧?
  那好,如果它前面加上1呢,仍然表示0?这不是重复了么?
  一个0,怎么用两个值来表示呢！！！
  所以1000 0000就表示-128啦，

ok，我们接下来就在8位二进制数，即-128~127的范围内取值来介绍它的原码、反码、补码

1、正数：原码、反码、补码都一样
   真值：3
   原码：0000 0011   最高位为0，表示正数
   反码：0000 0011
   补码：0000 0011

2、负数：原码、反码、补码不同
   真值：-3
   原码：1000 0011   最高位为1，表示负数
   反码：1111 1100   由原码演变而来，原码的符号位不变，数值位全部取反
   补码：1111 1101   在反码的基础上+1

为了大家能够清晰地看到”真值“与”补码“之间的相互转换，egon画了如下两幅图

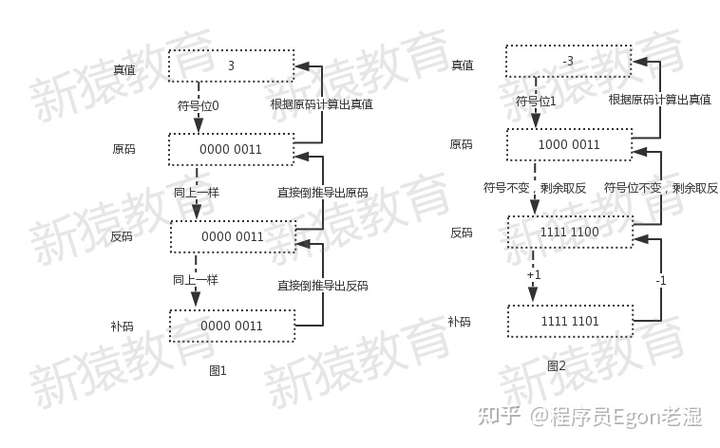
在计算机系统中，数值一律用补码来存储 ！！！ 主要原因：使用补码，可以将符号位和其它位统一处理；同时，减法也可按加法来处理，需要注意的是两个用 补码表示的数相加时，如果最高位（符号位）有进位，则进位被舍弃，处理完后我们如上图所示用补码反推出真值即可，例如计算机在计算8-3的时候，会这么做8+（-3），具体如下

第一步：真值->原码->反码->补码
    真值：8
    原码：0000 1000  
    反码：0000 1000
    补码：0000 1000

    真值：-3
    原码：1000 0011  
    反码：1111 1100
    补码：1111 1101

第二步：补码之间的运算，此处为相加
    8的补码：0000 1000
   -3的补码：1111 1101
  相加得补码：0000 0101 # 补码相加，高位有进位会被舍弃
    
第三步：补码->反码->原码->真值
    上一步得到的补码结果：0000 0101
    符号位是0，为正数，那么就简单了，正数的原、反、补码都一样，所以一步到位
    补码->反码->原码：0000 0101
    
    原码->真值：5

练习：8+（-9）

第一步：真值->原码->补码
    真值：8
    原码：0000 1000  
    反码：0000 1000
    补码：0000 1000

    真值：-9
    原码：1000 1001  
    反码：1111 0110
    补码：1111 0111

第二步：补码之间的运算，此处为相加
    8的补码：0000 1000
   -9的补码：1111 0111
  相加得补码：1111 1111 
    
第三步：补码->反码->原码->真值
 补码->反码
        补码结果：1111 1111
        符号位是1，为负数，参照上图2的步骤

        补码->反码：-1，得到反码：1111 1110
    
    反码->原码：符号位不变，其余位取反，得到原码：1000 0001
    
    原码->真值：-1

非常震撼人心的设计，有了补码以后，减法都可以当做加法去运算，你可知道，这将极大地简化计算机的运算设计。不仅如此！！！

我们即将介绍的位运算也都是基于补码进行的，所以，你还会觉得egon在啰嗦吗？呵呵

三 位运算

按位与&：两位全为1，结果才为1，否则为0
按位或|：两位只要存在一个1，结果就为1，否则为0
按位异或^：只有在两位不相同，即一个为0一个为1的情况下，结果才为1，否则为0
<< n：各二进制位全部左移n位，高位丢弃，低位补0
>> n: 各二进制位全部右移n位，如果是正数，则高位补0，如果是负数则高位补1

####3.1 按位与&

示例1：8 & -3

第一步：真值->原码->反码->补码
    真值：8
    原码：0000 1000  
    反码：0000 1000
    补码：0000 1000

    真值：-3
    原码：1000 0011  
    反码：1111 1100
    补码：1111 1101

第二步：补码之间的运算，此处为&
    8的补码：0000 1000
   -3的补码：1111 1101
    &得补码：0000 1000
    
第三步：补码->反码->原码->真值
    上一步得到的补码结果：0000 1000
    符号位是0，为正数，那么就简单了，正数的原、反、补码都一样，所以一步到位
    补码->反码->原码：0000 1000
    
    原码->真值：8

示例2：-8 & -9

第一步：真值->原码->补码
    真值：-8
    原码：1000 1000  
    反码：1111 0111
    补码：1111 1000

    真值：-9
    原码：1000 1001  
    反码：1111 0110
    补码：1111 0111

第二步：补码之间的运算，此处为&
   -8的补码：1111 1000
   -9的补码：1111 0111
    &得补码：1111 0000 
    
第三步：补码->反码->原码->真值
 补码->反码
        补码结果：1111 0000 
        符号位是1，为负数，参照上图2的步骤

        补码->反码：-1，得到反码：1110 1111
    
    反码->原码：符号位不变，其余位取反，得到原码：1001 0000
    
    原码->真值：-16

####3.2 按位或|

示例1：-8 | -9

第一步：真值->原码->补码
    真值：-8
    原码：1000 1000  
    反码：1111 0111
    补码：1111 1000

    真值：-9
    原码：1000 1001  
    反码：1111 0110
    补码：1111 0111

第二步：补码之间的运算，此处为|
   -8的补码：1111 1000
   -9的补码：1111 0111
    |得补码：1111 1111 
    
第三步：补码->反码->原码->真值
 补码->反码
        补码结果：1111 1111 
        符号位是1，为负数，参照上图2的步骤

        补码->反码：-1，得到反码：1111 1110
    
    反码->原码：符号位不变，其余位取反，得到原码：1000 0001
    
    原码->真值：-1

####3.3 按位异或^

示例1：-8 ^ -9

第一步：真值->原码->补码
    真值：-8
    原码：1000 1000  
    反码：1111 0111
    补码：1111 1000

    真值：-9
    原码：1000 1001  
    反码：1111 0110
    补码：1111 0111

第二步：补码之间的运算，此处为^
   -8的补码：1111 1000
   -9的补码：1111 0111
    ^得补码：0000 1111 
    
第三步：补码->反码->原码->真值
    上一步得到的补码结果：0000 1111
    符号位是0，为正数，那么就简单了，正数的原、反、补码都一样，所以一步到位
    补码->反码->原码：0000 1111
    
    原码->真值：15

示例2：^ -8 单独一个^代表取反的意思(适用于go，不适用于python)

第一步：真值->原码->补码
    真值：-8
    原码：1000 1000  
    反码：1111 0111
    补码：1111 1000

第二步：
   -8的补码：1111 1000
 ^取反得补码：0000 0111 
    
第三步：补码->反码->原码->真值
    上一步得到的补码结果：0000 0111
    符号位是0，为正数，那么就简单了，正数的原、反、补码都一样，所以一步到位
    补码->反码->原码：0000 0111
    
    原码->真值：7

####3.4 向左位移<< n

示范1：-8 << 3

第一步：真值->原码->补码
    真值：-8
    原码：1000 1000  
    反码：1111 0111
    补码：1111 1000

第二步：<< n 各二进制位全部左移n位，高位丢弃，低位补0
    补码：1111 1000
    <<3: 1100 0000

    
第三步：补码->反码->原码->真值
 补码->反码
        补码结果：1100 0000
        符号位是1，为负数，参照上图2的步骤

        补码->反码：-1，得到反码：1011 1111
    
    反码->原码：符号位不变，其余位取反，得到原码：1100 0000
    
    原码->真值：-64

####3.5 向右位移>> n

示范1：-8 >> 3

第一步：真值->原码->补码
    真值：-8
    原码：1000 1000  
    反码：1111 0111
    补码：1111 1000

第二步：>> n 各二进制位全部右移n位，如果是正数，则高位补0，如果是负数则高位补1
    补码：1111 1000
    >>3: 1111 1111

    
第三步：补码->反码->原码->真值
 补码->反码
        补码结果：1111 1111
        符号位是1，为负数，参照上图2的步骤

        补码->反码：-1，得到反码：1111 1110
    
    反码->原码：符号位不变，其余位取反，得到原码：1000 0001
    
    原码->真值：-1

示范2：8 >> 3

第一步：真值->原码->补码
    真值：8
    原码：0000 1000  
    反码：0000 1000
    补码：0000 1000

第二步：>> n 各二进制位全部右移n位，如果是正数，则高位补0，如果是负责则高位补1
    补码：0000 1000
    >>3: 0000 0001

    
第三步：补码->反码->原码->真值
    上一步得到的补码结果：0000 0001
    符号位是0，为正数，那么就简单了，正数的原、反、补码都一样，所以一步到位
    补码->反码->原码：0000 0001
    
    原码->真值：1

示范3：-300 >> 8

第一步：真值->原码->补码
    真值：-300  
    原码：1000 0001 0010 1100 # -300 已经超过了8位二进制能表示的范围，需要用16位表示
    反码：1111 1110 1101 0011
    补码：1111 1110 1101 0100

第二步：>> n 各二进制位全部右移n位，如果是正数，则高位补0，如果是负责则高位补1
    补码：1111 1110 1101 0100
    >>8: 1111 1111 1111 1110

    
第三步：补码->反码->原码->真值
 补码->反码
        补码结果：1111 1111 1111 1110
        符号位是1，为负数，参照上图2的步骤

        补码->反码：-1，得到反码：1111 1111 1111 1101
    
    反码->原码：符号位不变，其余位取反，得到原码：1000 0000 0000 0010
    
    原码->真值：-2

四 位运算高级操作

位运算是 cpu 直接支持的，效率最高，位运算可能在平常的编程中使用的并不多，但涉及到底层优化，一些算法及源码可能会经常遇见，下面来介绍一下风骚的操作

####4.1 用位运算 & 取代 % 取模

X % 2^n = X & (2^n – 1)
注意：用位运算 & 来取代 % 取模需要被取模的数必须是2的幂才成立

示范1：

10 % (2^3) 等于 10 & (2^3-1)
即
10 % 8 等于 10 & 7

示范2：

10 % (2^2) 等于 10 & (2^2-1)
即
10 % 4 等于 10 & 3

####4.2 将一个数左移 n 位，相当于乘以了 2 的 n 次方，右移n位，相当于除以2的n次方取整

10 << 3 等同于10 * 2^3 
10 >> 3 等同于10 / 3

4.3 判断奇偶

我们可以利用 & 运算符的特性，来判断二进制数第一位是0还是1。
用if ((a & 1) == 0) 代替 if (a % 2 == 0)来判断a是不是偶数。

4.4 交互数值

1、借助临时变量来交互数值

    a:=10
    b:=20

    temp:=a
    a=b
    b=temp

 fmt.Println(a,b) // 结果20 10
2、借助累加和
如果考虑到内存，不希望使用临时变量（其实就是为了炫酷），可以这样实现：

    a:=10
    b:=20

    a = a + b
    b = a - b
    a = a - b
    fmt.Println(a,b) // 结果20 10
    
从数学角度来分析一下
- 第一步：a = a + b
- 第二步：b = a - b = (a + b) - b = a
- 第三步：a = a - b = (a + b) - b = (a + b) - a = b

3、使用 ^ 位运算符
如果想要更炫酷一点可以使用 ^ 来帮忙实现：
先来了解一下 ^ 的几个特性：
a ^ a = 0
a ^ 0 = a
(a ^ b) ^ c = a ^ (b ^ c)

代码：
    a:=10
    b:=20

    a ^= b;
    b ^= a;
    a ^= b;
    fmt.Println(a,b) // 结果20 10


从数学角度来分析一下：
- 第一步：a = a ^ b
- 第二步：b = a ^ b = (a ^ b) ^ b = a ^ (b ^ b) = a ^ 0 = a
- 第三步：a = a ^ b = (a ^ b) ^ b = (a ^ a) ^ b = b ^ 0 = b

####4.5 项目中的应用

在项目中可以用位运算进行一些状态的运算，效率极其高，例如：现在我们有一些爱好需求，这些爱好有 足球 羽毛球 乒乓球 篮球 游泳 如果按照整数的形式去定义，那就有无数多种情况，毕竟可以两两组合嘛，python中的列表、go中的数组都不是最佳选择

可以直接用二进制位表示，1代表爱好，0代表没有该爱好

爱好：只有足球
表示：1 0 0 0 0


爱好：乒乓球、游泳
表示：0 0 1 0 1

接下来就可以用位运算进行一些风骚的操作啦，例如

#####应用1：检查是否存在某个爱好

喜欢足球的状态是：1 0 0 0 0 
     小明的喜好：0 1 0 1 0
 与&计算的结果为：0 0 0 0 0，返回位false，所以小明不存在喜好足球的状态

#####应用2：添加某个爱好

喜欢足球：   1 0 0 0 0
小明的喜好： 0 1 0 1 0 
或|运算之后： 1 1 0 1 0

应用3：移除某个爱好

（传入）喜好足球 ： 1 0 0 0 0

    小明的喜好：   1 0 1 0 1
先将足球取反^ ：   0 1 1 1 1
   再进与&运算：   0 0 1 0 1

以上风骚操作均适用于python！！！egon忙忙叨叨写了一天，希望能够帮助到你